C++ 코딩테스트 Week 03
용어 정리
Graph
정점(vertex): 노드라고도 불리며, 그래프를 형성하는 기본 단위
간선(Edge) : 정점을 잇는 선을 의미. 관계, 경로 등
- 단방향 간선 : vertex간 일방동행만 되는 edge
- 양방향 간선 : vertex간 이중통행이 되는 edge
- 무방향 간선 : 방향이 없는 edge
Indegree, Outdegree : 해당 vertex에서 in/out하는 edge의 개수
가중치(weight) : vertex와 vertex 사이의 비용
Graph : Vertex와 Edge로 이루어진 집합
Tree
트리(Tree) : 자식노드와 부모노드로 이루어진 계층적인 구조를 가지며, 무방향 그래프의 일종. 사이클이 존재하지 않는 자료구조를 의미
Tree 또한 vertex와 edge를 가지는 집합이므로, Graph의 이론이다.
Tree의 특징은 다음과 같다.
- 부모, 자식 계층 구조를 가진다.
- V - 1 = E
- 임의의 두 노드 사이의 경로는 유일하게 존재한다.
Root Node : 가장 위에 있는 노드. 보통 root node를 먼저 탐색하면 된다.
Inner Node : Root Node와 Leaf Node 사이의 노드를 의미
Leaf Node : 자식이 없는 노드
Depth(Level) : Root Node에서 특정 노드까지의 최단 거리의 거리
Height : Depth의 최댓값
Forest : Tree로 이루어진 집합
Binary Tree
각 자식 노드의 수가 2개 이하인 트리
- 정이진 트리(full binary tree): 자식 노드가 0 또는 2개인 이진 트리를 의미합니다.
- 완전 이진 트리(complete binary tree): 왼쪽에서부터 채워져 있는 이진 트리를 의미합니다. 마지막 레벨을 제외하고는 모든 레벨이 완전히 채워져 있으며 마지막 레벨의 경우 왼쪽부터 채워져 있습니다.
- 변질 이진 트리(degenerate binary tree): 자식 노드가 하나밖에 없는 이진 트리를 의미합니다.
- 포화 이진 트리(perfect binary tree): 모든 노드가 꽉 차 있는 이진 트리를 의미합니다.
- 균형 이진 트리(balanced binary tree): 모든 노드의 왼쪽 하위트리와 오른쪽 하위트리의 차이가 1이하인 트리입니다. map, set을 구성하는 레드블랙트리는 균형이진트리 중 하나입니다.
[출처] [알고리즘 강의] 2주차. 그래프이론, 인접행렬, 인접리스트, DFS, BFS, 트리순회 작성자 큰돌
Binary Search Tree(BST)
Binary Tree의 일종으로,
노드의 오른쪽 하위 트리에는 노드의 값보다 큰 값
왼쪽 하위 트리에는 노드의 값보다 작은 값이 있는 트리
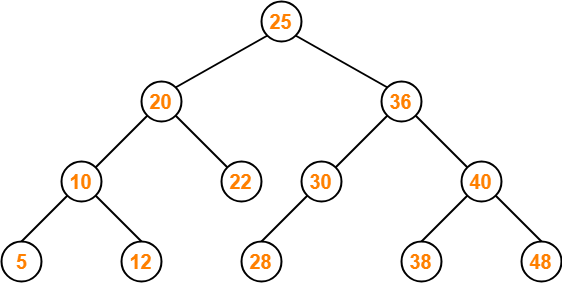
균형 잡힌 이진 트리의 탐색, 삽입, 삭제, 수정은 모두 시간 복잡도 O(logN)이다.
다른 이진 트리를 균형 잡힌 이진트리로 만들기 위해서 AVL tree, Red-Black tree 알고리즘이 존재한다.
Graph 구현 & 탐색
Adjacency Matrix
인접 행렬이란 그래프에서 정점과 간선의 관계를 나타내는 bool 타입의 정사각형 행렬
bool adj[4][4] = {
{0, 1, 1, 1},
{1, 0, 1, 0},
{1, 1, 0, 0},
{1, 0, 0, 0},
};
//여기서 0은 edge가 없음을, 1은 edge가 존재함을 나타낸다
bool adj[V][V]
for(int i = 0; i < V; i++){
for(int j = 0; j < V; j++){
if(adj[i][j]){
cout<<i<<" and "<<j<<"is conntected"<<endl;
bfs(i);
dfs(i);
}
}
}
인접 행렬을 이용한 예제 코드
#include <stdio.h>
#include <iostream>
using namespace std;
const int V=10;
bool adj[V][V], visited[V];
void go(int from){
visited[from]=1;
cout<<from<<" is visited"<<endl;
for(int i=0;i<V;i++){
if(adj[from][i]&&!visited[from]){
go(i);
}
}
}
int main(){
adj[1][2]=1; adj[1][3]=1; adj[3][4]=1;
adj[2][1]=1; adj[3][1]=1; adj[4][3]=1;
for(int i=0;i<V;i++){
for(int j=0;j<V;j++){
if(adj[i][j]&!visited[i]){
go(i);
}
}
}
return 0;
}
Adjacency List
인접 리스트(adjacenct list)란 그래프에서 vertex와 edge의 관계를 나타내는 연결 리스트를 의미
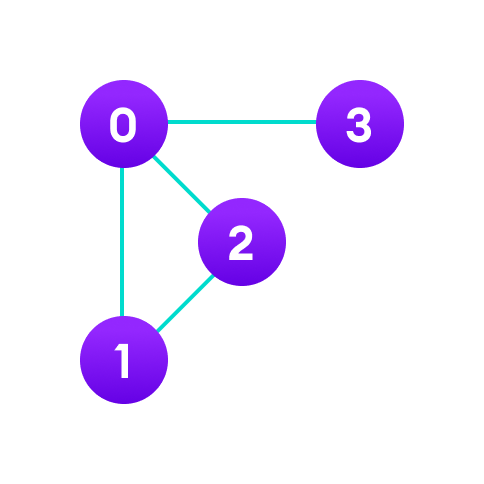
위 그래프를 인접리스트로 아래와 같이 나타낼 수 있음
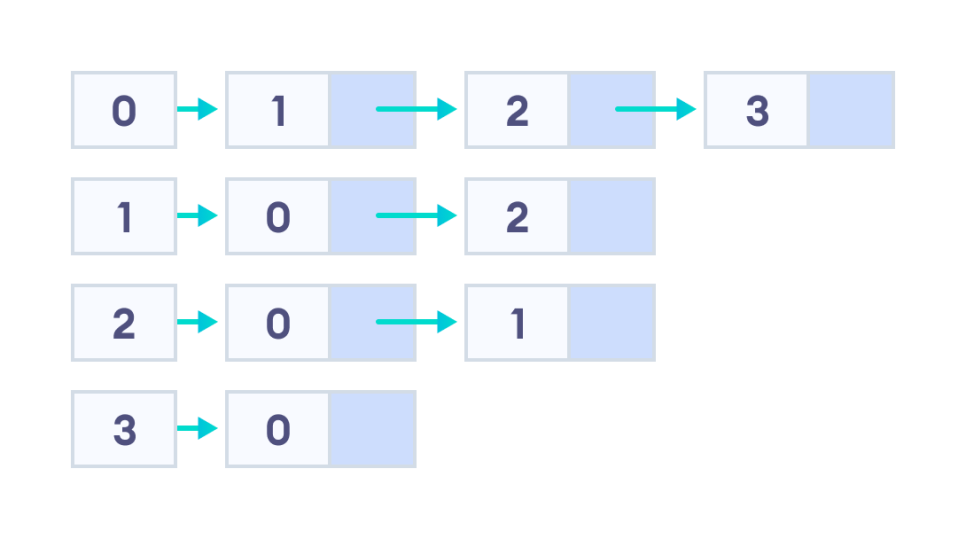
코드로 구현하면 아래와 같음
#include <iostream>
#include <vector>
using namespace std;
const int V=4;
vector<int> adj[V];
int main(){
//init adjacency lists
adj[0].push_back(1);
adj[0].push_back(2);
adj[0].push_back(3);
adj[1].push_back(0);
adj[1].push_back(2);
adj[2].push_back(0);
adj[2].push_back(1);
adj[3].push_back(0);
for(int i=0;i<4;i++){
cout<< i <<" :: ";
for(int there : adj[i]){
cout<<there<<" ";
}
cout<<"\n";
}
// another version
// for(int i=0;i<V;i++){
// cout<<i<<" :: ";
// for(int j=0;j<adj[i].size();j++){
// cout<<adj[i][j];
// }
// cout<<"\n";
// }
return 0;
}
연결리스트를 구현할때 vector로 구현해도 무방하다.
인접리스트에 구현할 때 많이 사용되는 연산은 마지막 연산에 삽입과 해당 배열을 탐색하는 것인데, vector와 list모두 각각 O(1), O(n)의 시간이 동일하게 들기 때문이다.
예제 코드
#include <iostream>
#include <vector>
using namespace std;
const int V=10;
vector<int> adj[V];
bool visited[V];
void go(int idx){
cout<<idx<<" ";
visited[idx] = true;
for(int there : adj[idx]){
if(visited[there]) continue;
go(there);
}
return;
}
int main(){
//init adjacency lists
adj[1].push_back(2);
adj[1].push_back(3);
adj[2].push_back(1);
adj[3].push_back(1);
adj[3].push_back(4);
adj[4].push_back(3);
//print adjacency lists
for(int i=0; i<V; i++){
if(adj[i].size()&&!visited[i]) go(i);
}
return 0;
}
인접 행렬과 인접 리스트의 공간 복잡도
-
인접 행렬의 공간 복잡도 : O(V^2)
-
인접 리스트의 공간 복잡도 : O(V+E)
그래프가 희소할 떄는 인접 리스트, 조밀할 때는 인접 행렬이 좋다.
따라서 보통은 인접 리스트로 푸는게 합리적 (메모리 절약 측면)

Leave a comment